Publications
Publications by categories in reversed chronological order.
Journal Articles
2025
- JCPMultilevel Matrix-Free Method for High-Performance Isogeometric Analysis of Lattice StructuresJournal of Computational Physics, Sep 2025
This paper presents a novel high-performance solver for the isogeometric analysis of lattice structures, designed to jointly exploit distributed-memory computing architectures and the specific nature of the problem. This work breaks with conventional approaches that primarily focus on multiscale homogenization or structural elements like beams and shells. Instead, it introduces a solver capable of meeting the overwhelming computational demands of full high-fidelity, fine-scale simulations of lattice structures. The solver features a two-level geometric preconditioner with a fine-level smoother based on overlapping domain decomposition, and a coarse-level correction utilizing an algebraic multigrid method. By leveraging the multiscale nature of the lattice structures, a matrix-free approach is employed at the fine level to perform matrix-vector products and apply transfer operators based on spline k-refinement. The structural similarities of the cells are also exploited through a reduced-order modeling procedure applied within each subdomain, which is used to efficiently compute the corresponding local solves within the fine-level smoother. A series of numerical experiments in both 2D and 3D, spanning various micro- and macro-geometries, are conducted to evaluate the efficiency of the solver in terms of memory usage, computational time, and robustness with respect to mesh refinement, spline degree, and problem size. Notably, an industrially representative spiral channel regenerative cooling thrust chamber lattice structure, consisting of over 66000 cells, is simulated in minutes using thousands of processes.
@article{guilletMultilevelMatrixfreeMethod2025, title = {Multilevel Matrix-Free Method for High-Performance Isogeometric Analysis of Lattice Structures}, author = {Guillet, C. and Hirschler, T. and Jolivet, P. and Bouclier, R.}, year = {2025}, month = sep, journal = {Journal of Computational Physics}, volume = {537}, pages = {114136}, issn = {00219991}, doi = {10.1016/j.jcp.2025.114136}, } - IJSolStrAn Optimal Penalty Method for the Joint Stiffening in Beam Models of Additively Manufactured Lattice StructuresInternational Journal of Solids and Structures, Jan 2025
Additive manufacturing is revolutionizing structural design, with lattice structures becoming increasingly prominent due to their superior mechanical properties. However, simulating these structures quickly and accurately using the finite element method (FEM) remains challenging. Recent research has highlighted beam element simulation within FEM as a more efficient alternative to traditional solid FE simulations, achieving similar accuracy with reduced computational resources. However, a significant challenge is managing the lack of rigidity at nodes and the prevalence of low aspect ratio beams. While various methodologies have been proposed to address these issues, there is still a gap in the comprehensive evaluation of their limitations. An optimal node penalization methodology is required to expand the limited range of accurately represented lattice behavior. A preliminary study investigates lattice geometries through comparative analysis of solid and beam FE simulations. Built on this, we developed a methodology suitable to linear, dynamics and nonlinear beam FE simulations, contributing to enhanced computational speed and accuracy. Several lattice structures were printed using material jetting and quasi-static compressive tests were conducted to validate the methodology’s accuracy. The numerical results reveal a good accuracy between the proposed beam FE methodology and the experimental data, offering a better alternative to conventional FEM for energy absorption in terms of computing time.
@article{cadartOptimalPenaltyMethod2024, title = {An Optimal Penalty Method for the Joint Stiffening in Beam Models of Additively Manufactured Lattice Structures}, author = {Cadart, T. and Hirschler, T. and Bahi, S. and Roth, S. and Demoly, F. and Lebaal, N.}, year = {2025}, month = jan, journal = {International Journal of Solids and Structures}, volume = {306}, pages = {113107}, issn = {00207683}, doi = {10.1016/j.ijsolstr.2024.113107}, }
2024
- IJNMEReduced Order Modeling Based Inexact FETI-DP Solver for Lattice StructuresInternational Journal for Numerical Methods in Engineering, Jan 2024
This paper addresses the overwhelming computational resources needed with standard numerical approaches to simulate architected materials. Those multiscale heterogeneous lattice structures gain intensive interest in conjunction with the improvement of additive manufacturing as they offer, among many others, excellent stiffness-to-weight ratios. We develop here a dedicated HPC solver that benefits from the specific nature of the underlying problem in order to drastically reduce the computational costs (memory and time) for the full fine-scale analysis of lattice structures. Our purpose is to take advantage of the natural domain decomposition into cells and, even more importantly, of the geometrical and mechanical similarities among cells. Our solver consists in a so-called inexact FETI-DP method where the local, cell-wise operators and solutions are approximated with reduced order modeling techniques. Instead of considering independently every cell, we end up with only few principal local problems to solve and make use of the corresponding principal cell-wise operators to approximate all the others. It results in a scalable algorithm that saves numerous local factorizations. Our solver is applied for the isogeometric analysis of lattices built by spline composition, which offers the opportunity to compute the reduced basis with macro-scale data, thereby making our method also multiscale and matrix-free. The solver is tested against various 2D and 3D analyses. It shows major gains compared to black-box solvers; in particular, problems of several millions of degrees of freedom can be solved with a simple computer within few minutes.
@article{hirschlerReducedOrderModeling2024, title = {Reduced Order Modeling Based Inexact {{FETI}}-{{DP}} Solver for Lattice Structures}, author = {Hirschler, T. and Bouclier, R. and Antolin, P. and Buffa, A.}, year = {2024}, journal = {International Journal for Numerical Methods in Engineering}, volume = {125}, number = {8}, pages = {e7419}, issn = {0029-5981, 1097-0207}, doi = {10.1002/nme.7419}, }
2022
- EWCO
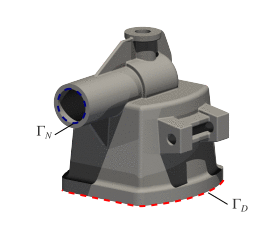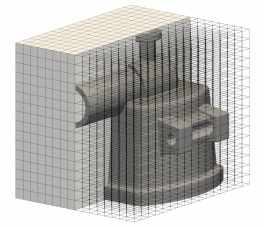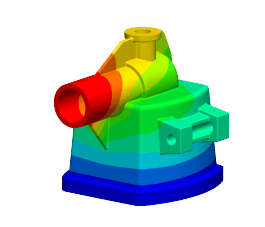Quadrature-Free Immersed Isogeometric AnalysisP. Antolin, and T. HirschlerEngineering with Computers, Oct 2022This paper presents a novel method for solving partial differential equations on three-dimensional CAD geometries by means of immersed isogeometric discretizations that do not require quadrature schemes. It relies on a newly developed technique for the evaluation of polynomial integrals over spline boundary representations that is exclusively based on analytical computations. First, through a consistent polynomial approximation step, the finite element operators of the Galerkin method are transformed into integrals involving only polynomial integrands. Then, by successive applications of the divergence theorem, those integrals over B-Reps are transformed into the first surface and then line integrals with polynomials integrands. Eventually, these line integrals are evaluated analytically with machine precision accuracy. The performance of the proposed method is demonstrated by means of numerical experiments in the context of 2D and 3D elliptic problems, retrieving optimal error convergence order in all cases. Finally, the methodology is illustrated for 3D CAD models with an industrial level of complexity.
@article{antolinQuadraturefreeImmersedIsogeometric2022, title = {Quadrature-Free Immersed Isogeometric Analysis}, author = {Antolin, P. and Hirschler, T.}, year = {2022}, month = oct, journal = {Engineering with Computers}, volume = {38}, number = {5}, pages = {4475--4499}, issn = {0177-0667, 1435-5663}, doi = {10.1007/s00366-022-01644-3}, } - CMFast and Multiscale Formation of Isogeometric Matrices of Microstructured Geometric ModelsT. Hirschler, P. Antolin, and A. BuffaComputational Mechanics, Feb 2022
The matrix formation associated to high-order discretizations is known to be numerically demanding. Based on the existing procedure of interpolation and lookup, we design a multiscale assembly procedure to reduce the exorbitant assembly time in the context of isogeometric linear elasticity of complex microstructured geometries modeled via spline compositions. The developed isogeometric approach involves a polynomial approximation occurring at the macro-scale and the use of lookup tables with pre-computed integrals incorporating the micro-scale information. We provide theoretical insights and numerical examples to investigate the performance of the procedure. The strategy turns out to be of great interest not only to form finite element operators but also to compute other quantities in a fast manner as for instance sensitivity analyses commonly used in design optimization.
@article{hirschlerFastMultiscaleFormation2022, title = {Fast and Multiscale Formation of Isogeometric Matrices of Microstructured Geometric Models}, author = {Hirschler, T. and Antolin, P. and Buffa, A.}, year = {2022}, month = feb, journal = {Computational Mechanics}, volume = {69}, number = {2}, pages = {439--466}, issn = {0178-7675, 1432-0924}, doi = {10.1007/s00466-021-02098-y}, }
2021
- ACMEA New Lighting on Analytical Discrete Sensitivities in the Context of IsoGeometric Shape OptimizationArchives of Computational Methods in Engineering, Jun 2021
Isogeometric shape optimization has been now studied for over a decade. This contribution aims at compiling the key ingredients within this promising framework, with a particular attention to sensitivity analysis. Based on all the researches related to isogeometric shape optimization, we present a global overview of the process which has emerged. The principal feature is the use of two refinement levels of the same geometry: a coarse level where the shape updates are imposed and a fine level where the analysis is performed. We explain how these two models interact during the optimization, and especially during the sensitivity analysis. We present new theoretical developments, algorithms, and quantitative results regarding the analytical calculation of discrete adjoint-based sensitivities. In order to highlight the versatility of this sensitivity analysis method, we perform eight benchmark optimization examples with different types of objective functions (compliance, displacement field, stress field, and natural frequencies), different types of isogeometric element (2D and 3D standard solids, and a Kirchhoff–Love shell), and different types of structural analysis (static and vibration). The numerical performances of the analytical sensitivities are compared with approximate sensitivities. The results in terms of accuracy and numerical cost make us believe that the presented method is a viable strategy to build a robust framework for shape optimization.
@article{hirschlerNewLightingAnalytical2021, title = {A {{New Lighting}} on {{Analytical Discrete Sensitivities}} in the {{Context}} of {{IsoGeometric Shape Optimization}}}, author = {Hirschler, T. and Bouclier, R. and Duval, A. and Elguedj, T. and Morlier, J.}, year = {2021}, month = jun, journal = {Archives of Computational Methods in Engineering}, volume = {28}, number = {4}, pages = {2371--2408}, issn = {1134-3060, 1886-1784}, doi = {10.1007/s11831-020-09458-6}, }
2019
- CMAMEA Dual Domain Decomposition Algorithm for the Analysis of Non-Conforming Isogeometric Kirchhoff–Love ShellsComputer Methods in Applied Mechanics and Engineering, Dec 2019
Originally, Isogeometric Analysis is aimed at using geometric models for the structural analysis. The actual realization of this objective to complex real-world structures requires a special treatment of the non-conformities between the patches generated during the geometric modeling. Different advanced numerical tools now enable to analyze elaborated multipatch models, especially regarding the imposition of the interface coupling conditions. However, in order to push forward the isogeometric concept, a closer look at the algorithm of resolution for multipatch geometries seems crucial. Hence, we present a dual Domain Decomposition algorithm for accurately analyzing non-conforming multipatch Kirchhoff–Love shells. The starting point is the use of a Mortar method for imposing the coupling conditions between the shells. The additional degrees of freedom coming from the Lagrange multiplier field enable to formulate an interface problem, known as the one-level FETI problem. The interface problem is solved using an iterative solver where, at each iteration, only local quantities defined at the patch level (i.e. per sub-domain) are involved which makes the overall algorithm naturally parallelizable. We study the preconditioning step in order to get an algorithm which is numerically scalable. Several examples ranging from simple benchmark cases to semi-industrial problems highlight the great potential of the method.
@article{hirschlerDualDomainDecomposition2019, title = {A Dual Domain Decomposition Algorithm for the Analysis of Non-Conforming Isogeometric {{Kirchhoff}}--{{Love}} Shells}, author = {Hirschler, T. and Bouclier, R. and Dureisseix, D. and Duval, A. and Elguedj, T. and Morlier, J.}, year = {2019}, month = dec, journal = {Computer Methods in Applied Mechanics and Engineering}, volume = {357}, pages = {112578}, issn = {00457825}, doi = {10.1016/j.cma.2019.112578}, } - CMAMEThe Embedded Isogeometric Kirchhoff–Love Shell: From Design to Shape Optimization of Non-Conforming Stiffened Multipatch StructuresComputer Methods in Applied Mechanics and Engineering, Jun 2019
Isogeometric shape optimization uses a unique model for the geometric description and for the analysis. The benefits are multiple: in particular, it avoids tedious procedures related to mesh updates. However, although the analysis of complex multipatch structures now becomes tractable with advanced numerical tools, isogeometric shape optimization has not yet been proven to be applicable for designing such structures. Based on the initial concept of integrating design and analysis, we develop a new approach that deals with the shape optimization of non-conforming multipatch structures. The model is built by employing the Free-Form Deformation principle. Introducing NURBS composition drastically simplifies the imposition of the shape updates in case of a non-conforming multipatch configuration. In the case of stiffened structures, the use of embedded surfaces enables to tackle the geometric constraint of connecting interfaces between the panel and the stiffeners during shape modifications. For the analysis, we introduce the embedded Kirchhoff–Love shell formulation. The NURBS composition defines the geometry of the shell while the displacement field is approximated using the same spline functions as for the embedded surface. We also formulate a new mortar method to couple non-conforming Kirchhoff–Love shells which intersect with any angle. We apply the developed method on different examples to demonstrate its efficiency and its potential to optimize complex industrial structures in a smooth manner.
@article{hirschlerEmbeddedIsogeometricKirchhoff2019, title = {The Embedded Isogeometric {{Kirchhoff}}--{{Love}} Shell: {{From}} Design to Shape Optimization of Non-Conforming Stiffened Multipatch Structures}, author = {Hirschler, T. and Bouclier, R. and Duval, A. and Elguedj, T. and Morlier, J.}, year = {2019}, month = jun, journal = {Computer Methods in Applied Mechanics and Engineering}, volume = {349}, pages = {774--797}, issn = {00457825}, doi = {10.1016/j.cma.2019.02.042}, } - SAMO
Isogeometric Sizing and Shape Optimization of Thin Structures with a Solid-Shell ApproachStructural and Multidisciplinary Optimization, Jun 2019This work explores the use of solid-shell elements in the the framework of isogeometric shape optimization of shells. The main difference of these elements with respect to pure shell ones is their volumetric nature which can provide recognized benefits to analyze, for example, structures with non-linear behaviors. From the design point of view, we show that this geometric representation of the thickness is also of great interest since it offers new possibilities: continuous sizing variations can be imposed by modifying the distance between the control points of the outer surfaces. In other words, shape and sizing optimization can be performed in an identical manner. Firstly, we carry out a range of numerical experiments in order to carefully compare the results with the commonly adopted technique based on the Kirchhoff-Love formulation. These studies reveal that both solid-shell and Kirchhoff-Love strategies lead to very similar optimal shapes. Then, we apply a bi-step strategy to integrate shape and sizing optimization. We highlight the potential of the proposed approach on a stiffened cylinder where the cross section along the stiffener is optimized leading to a final design with smooth thickness variations. Finally, we combine the benefits of both Kirchhoff-Love and solid-shell formulations by setting up a multi-model optimization process to efficiently design a roof.
@article{hirschlerIsogeometricSizingShape2019, title = {Isogeometric Sizing and Shape Optimization of Thin Structures with a Solid-Shell Approach}, author = {Hirschler, T. and Bouclier, R. and Duval, A. and Elguedj, T. and Morlier, J.}, year = {2019}, journal = {Structural and Multidisciplinary Optimization}, volume = {59}, number = {3}, pages = {767--785}, doi = {10.1007/s00158-018-2100-6}, }
Books
2022
- WileyIGA: Non-conforming Coupling and Shape Optimization of Complex Multipatch StructuresRobin Bouclier, and Thibaut HirschlerJun 2022